[논문리뷰] Bank Runs, Deposit Insurance, and Liquidity (Diamond and Dybvig)

10월 10일,

Ben S. Bernanke, Douglas W. Diamond, Philip H. Dybvig 교수가

2022 노벨 경제학상을 수상했다.

이번 경제학상은

'for research on banks and financial crises'

라는 타이틀을 달고 있는데,

 

과연 이들은

은행과 금융위기와 관련해

어떤 연구를 진행한 것일까?

---

이번에 리뷰할 논문은

Douglas W. Diamond and Philip H. Dybvig (1983), Bank Runs, Deposit Insurance, and Liquidity, Journal of Political Economy, 91(3), 401-419이다.

 

이 논문은 경제학도들이

다이아몬드 - 디빅 모형이라고 부르는

뱅크런 모델이 다뤄진 논문이다.

 

이를 모델의 가정부터 천천히 살펴보면

다음과 같다.

우선 기간(T)은 세 개이다.

 

 

(이 가정은 현실을 단순화 한 것으로,
간단하게 1기는 현재, 2기는 미래로 생각해도 좋다.)

소비자들은 0기에 1단위의 부존자원을 가지고 있다.
이 재화를 0기에 투자하면 2기에 R > 1 만큼의 수익을 얻을 수 있다.
투자된 자금을 1기에 회수하면 투자안이 중단되어
1개의 재화를 그대로 돌려받는다.
단, 해당 경제는 3기까지만 존재하므로,
1기에 투자가 중단되면
다시 투자할 수 없다.

이 경제에는
참을성 없는 소비자(투자를 하지 않고, 1기에 재화를 소비하는 타입)
참을성 있는 소비자(투자를 하는 타입)
두 가지 타입의 소비자가 존재한다.
(이를 앞으로는 각각 타입1, 타입2 라고 표현하도록 한다.)
각 소비자들의 효용함수는 다음과 같이 나타낼 수 있다.(1기에 측정)

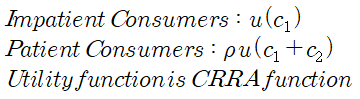
여기서 타입2 소비자가 투자 할 유인의 부여를 위해

이라고 가정하자.

---

이 상황에서 경쟁균형은
0기에 소비자들은 모두 부존자원을 투자하지만
타입1 소비자는 투자를 중단하고, 1기에 1의 재화를 소비하고,
타입2 소비자는 투자를 지속하여, 2기에 R의 재화를 소비하는 것이다.
(두 타입의 소비자 모두 해당 균형점에서 움직일 유인이 사라지는
Nash Equilibrium이다.)

경쟁균형은 이처럼 별도의 시장이 없는 상태에서도
달성 가능하다.

---

그렇다면 경쟁균형이 아닌,
사회적 효용이 최대가 되는 분배상태는 어떨까?

경제 내에 타입1이 t만큼,
타입2가 1-t 만큼 존재한다는 사실이
사전에 알려져 있는 정보라고 하자.
이 정보를 토대로
Social Planner의 입장에서 최적 배분을 구해보면 다음과 같다.

이는 소비자 타입의 특성상

라는 사실을 반영한 사회적 효용 극대화 식이다.

여기서 제약조건은
타입1 소비자가 1기에 소모하는 양을 제외한
나머지 재화(타입2 소비자의 재화)가 1기에 투자되고,
그 투자된 재화가 2기에 R배만큼 늘어난 양이
참을성 있는 소비자의 2기 소비와 같아야 한다는 의미이다.

이 극대화 문제를 풀이해보면,
1계조건은

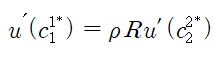
이며, 가정에 의해

이므로,

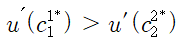
가 되고, 효용함수의 형태를 고려해보면
최적 배분은

의 조건을 만족하는 상태가 된다.

경쟁균형에 비해서는
타입1 소비자의 재화 소비량 1에서 증가했고,
타입2 소비자의 재화 소비량이 R에서 감소했음을 알 수 있다.

즉, Social Planner 문제에서
사회 효용을 극대화 시키는
최적의 배분은 경쟁균형에 비해
기간 1에 투자사업의 청산을 더 많이 요구하는 것이다.

---

금융 시장은
그 존재만으로 Social Planner의
사회 효용의 최적 상태를 이끌어 낼 수 있다.

금융 시장의 대표적인 형태인 은행의 예금 계약을
다음과 같은 형태로 가정해보자.
소비자들이 0기에 1을 예금하면,

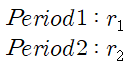
를 제공하는 예금 계약이 존재한다고 하자.
은행은 0기에 받은 금액을 모두 투자하게 된다.

모든 소비자들이 0기에 부존자원 1을 모두 예금하고,
1기에 인출하는 소비자 비율을 f라 하면,

의 조건이 만족되어야 할 것이고,
이 경우, 은행은 2기에

의 투자 수익을 올리게 되고, 1-f 비율의 소비자들이 이를 나눠 가지게 된다.

정의에 의해서
참을성 없는 소비자들은 2기보다는 1기의 소비를 좋아한다.
따라서 1기에 남는 자본은

가 되고, 은행이 2기에 얻게 되는 투자수익은

이 된다.

이 때 참을성 있는 소비자들은
1기에 인출하지 않고, 참았다가 2기에 인출할 유인이 생기는데,
이는 2기에 해당 소비자들이

만큼 소비를 하게 됨을 의미한다.
이 때, 2기에 소비되는 양은 1보다는 크기 때문에,
은행의 예금계약에서

이면, 타입2 소비자는 1기에 인출할 유인 없이
예금계약을 2기까지 유지하게 될 것이다.

은행은 이러한 예금 계약을 유지하는데 어려움이 없고,
두 타입의 소비자 모두
은행에 예금을 하는 것이
부존자원을 그대로 가지고 있는 경우에 비해
효용이 감소하지는 않기 때문에
최소 무차별한 상황으로 0기에 예금을 하는 상황에서 벗어날 유인이 없다.

즉, 은행이 예금계약을 도입한 것만으로
모두가 좋아지는 경쟁균형의 상태가
자연스레 성립되는 것이다.

여기서 재미있는 것은

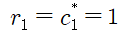
의 예금계약이 있으면,
정확히 경쟁균형과 같은 결과를 가지고 오게 된다는 사실이다.

위의 수식을 풀어보면
2기에 타입2 소비자가 소비하는 재화의 양은
정확히 R이 되기 때문이다.

---

그러나 위에서 본 균형은
은행의 예금 계약이 있는 경제에 존재하는
유일한 Nash Equilibrium이 아니다.

만약 1기에 두 타입의 소비자 모두 인출할 유인이 있다면
은행은 본인들이 가능한 것 이상으로 유동성 압박을 받게 된다.

1기에 인출이

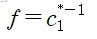
만큼 이루어지면, 1기 은행에 남는 자본은 없다.
따라서 2기에 줄 돈이 사라지게 되고,
결국 2기에 인출하고자 하는 소비자들,
즉

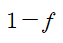
만큼의 사람들은 아무것도 인출하지 못하게 될 것이다.

타입1 소비자들(t)은 언제나 1기에 인출한다.
타입2 소비자들이 만약 1기에 인출하게 되면,
모두가 1기에 인출할 유인을 가지게 된다.

그들은 2기까지 기다리지 않고,
일찍 인출한다해도
부존자원으로 가지고 있던만큼을 1기에 소비하는 것으로
전혀 손해 볼 것이 없기 때문이다.

따라서 1기에 모두 인출하는 이 상태 역시
Nash Equilibrium이다.

를 뱅크런이 발생할 확률이라 가정하면,
이 때 사회 전체의 기대효용은

이고,

가 매우 낮은 상황이어서,

이런 부등식이 성립한다면,
은행 계약이 있는 부등식 앞의 사회가
경쟁균형이 있는 부등식 뒤의 사회보다
보다 높은 기대효용을 주는 바람직한 사회일 것이다.

하지만
살펴본 것처럼 은행 계약이 있는 사회에서는
분명 2기에 아무것도 받지 못하는 사람이 있는
우울한 사회이기도 하다.
이를 방지하기 위한 수단은 없을까?

---

위에서 살펴본 뱅크런 균형의 핵심은
은행이 1기에
소비자들이 요구하는대로 모두 다 지급을 해주고,
이 상황에서 결국 타입2 소비자들이
미래에 받을 자원이 없을 것을 예상하게 되면서,
그들이 1기에 인출하는 것을 막을 수 없다는 점에 있다.

따라서 가장 간단한 해법은
2기에 유동성제약을 겪지 않는 선을 정하고,
그 선에 맞춰 1기에 은행이 인출을 막는 것이다. (Suspension Contract)

그 비율의 조건은

이 될 것이다.

이 Suspension Contract 내에서는
타입1 소비자들은 언제나 인출을 하려 할 것이고(t)
타입2 소비자들은 1기에 인출을 하면,

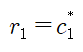
만큼 받을수도 있겠지만,
돈을 인출하는 사람들이 많아져
인출하는 비율 f가
은행이 정해놓은 비율을 넘어버리면
1기에 인출을 못하고,
2기의 인출을 기다리게 된다는 사실을 고려하여 결정하게 된다.

그러나 그들은 f가 줄어들면,
즉 본인들이 1기에 인출을 덜 하면,
본인들이 받을 수 있는 2기의 값이 증가한다는 사실을
잘 알고 있다. (Patient Consumers.)

이러한 상황을 고려하여
1기에 인출하는 사람들의 비율이
은행이 정한 비율과 동일하여
1기에 인출이 최대로 일어나는 상황을 살펴보자.

은행이 그 비율을 정확히 t로 정한다면,
사회는
타입 1 소비자들만 인출하고
타입 2는 모두 인출하지 않는

의 앞서 살펴본 Nash Equilibrium을 자연스레 달성하게 될 것이다.

또한 은행이 그 비율을 정할 때,
타입 2의 사람들이 1기에 인출하지 않고
인내할 수 있도록 유인을 부여하는 범위인

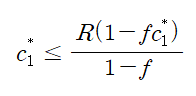
를 고려하여

에서 부여한다면, 타입 2 소비자들은
2기에 예상되는 소비의 효용이 더 크기 때문에
1기에 인출하지 않을 유인이 있다.

따라서 은행은

의 범위에서 1기 인출 제한 비율을 설정한다면,
뱅크런이라는 최악의 경우를 훌륭히 배제할 수 있다.

---

뱅크런을 방지하는 또 다른 방법은
소비자의 예금을 보장해주는 것이다.

정부기관에서 1기에
최적 사회 효용을 얻기 위해 세금을 부과할 수 있는
사회를 가정하자.
(이는 예금보험공사가 은행으로부터
예금보험료를 받는 형태를 떠올려도 될 것이다.)

이 세금은 1기에 인출하려는 소비자의 수에 기반하여
다음과 같이 매겨지게 되는 형태이다.

현재 이 사회의 은행계약 균형은

인 상태임을 고려하면

타입1 소비자의 경우,
세금까지 고려한 실제 소비량이
최소 0기에 가지고 있는 부존자원인 1보다
적지 않아야
은행에 저축을 할 것이다.

즉,
타입1 소비자만 인출한다면, 세금은 0이 부과 될 것이므로,
예금 계약에 의해 1보다 높은 소비를 기대할 수 있을 것이고,

타입2 소비자도 인출한데면,
부과되는 세금을 고려했을 때,

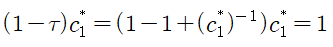
이 성립하므로,
1보다 낮지 않은 소비를 기대할 수 있다.

따라서 타입 1 소비자는
이 은행의 예금 계약을 가입할 유인이 여전히 존재한다.

이 때 실제 1기에 인출되는 비율(f)이
f=t 라면,
1기에 타입 1 소비자만 인출 했다는 의미로
예금보험 계약조건에 의해
세율은 0이 부과될 것이고,

자연스레 타입 2 소비자는
2기에

의 소비를 1기의 소비보다 선호하게 되면서
우리가 원하는
바람직한 Nash Equilibrium을 달성할 수 있게된다.

만약 f>t 면
타입 2 소비자 중 일부도 1기에 인출했다는 의미가 되며,
세율은 1기에

만큼 부과될 것이다.

타입 1 소비자의 경우는,
이 경우에도 예금가입을 유인할만한 조건으로
예금보장을 해주고 있으니,
여전히 예금계약을 유지할 것이다.

타입 2 소비자의 경우
1기의 최적 소비값이 1이므로,
결국
2기의 소비값은 R을 기대하게 된다.

따라서 타입2 소비자 역시
예금계약을 가입하고,
2기까지 기다릴 유인이 있는 셈이다.

이처럼
이와 같은 형태의 예금 보험 계약을 도입하는 것만으로
사회는 뱅크런 균형을 피해갈 수 있게 된다.

이러한 형태의 예금 보험 계약은
Suspension Contract 때,
t의 비율을 사전적으로 알고,
설정해야 했던것과는 다르게
그 비율을 사전에 모르고 1기에 실제 얼마나 인출되는지 본 후
그에 맞춰 행동하는 것을 약속하는 것만으로도
사회적 최적 균형을 달성할 수 있게 해준다는 점에서
의미가 깊다.

---

노벨 경제학상까지 받은
기념비적인 논문을
이해한 내용을 살려 보다 간단한 형태로 리뷰해보았다.

1983년에 이런 천재적인 발상을 하고,
우리 세상을
간단한 포인트들을 살려 단순히 모델화하여
세상에 큰 도움이 되는 유의미한 결론을 이끌어 낸
해당 페이퍼는
'for research on banks and financial crises'
라는 내용으로 노벨경제학상을 받는데 전혀 부족함이 없는 논문이다.

이런 연구는 생애 못해내더라도,
세상에 조금이라도 보탬이 될 만한 연구를
할 수 있었으면 좋겠다는
생각이 드는 하루다.